이번 포스팅에서는 토픽모델링(Topic modeling) 알고리즘 중 대표적인 Latent Dirichlet Allocation (잠재 디리클레 할당, LDA)알고리즘을 알아보고, R로 구현해보겠습니다.
살다보니 R을 쓰게되는 날도 오네요. 물론 아직 Python이 훨씬 편하긴 합니다, 앞으로도 계속 Python을 이용할 것 같구요…
Brief history of LDA
토픽모델링은 “대량의 문서에서 Topic(주제)를 추출하는 것” 정도로 요약할 수 있을것 같습니다.
최근의 텍스트분석에서는 수만개 이상의 문서에서 어떤 정보를 요약하고 추출하고 있습니다. 토픽모델링을 이용하면 이런 대량의 문서들이 주로 무엇에 대하여 이야기 하고 있는지, 각 문서들은 어떤 주제를 중심적으로 이야기 하는지 등을 알 수 있습니다.
토픽모델링과 관련하여 그 기원은 SVD(Singular value decomposition)으로 보는게 일반적입니다. SVD는 차원축소(Data dimension reduction)방법 중 하나로 어떤 행렬을 분해하는 방법입니다.
일반적으로 A=U*S*V^T 로 표기하는데 SVD에 대한 자세한 설명은 본 포스팅에서 할것이 아니니 넘어가고, 어쨋든 행렬 A를 문서-단어의 관계를 나타내는 행렬이라고 하면 U*S는 문서와 잠재변수의 관계를 나타내는 행렬, S*V^T는 잠재변수와 단어의 관계를 나타내는 행렬로 볼 수 있는데 이를 Latent semantic indexing(LSI)이라고 합니다.
그러나 LSI의 결과로 도출되는 두 행렬의 값은 직관적으로 이해하고 해석하기가 쉽지 않습니다. 그래서 이를 확률로 표현할수 있는 방법이 제시되었는데 이를 pLSI라고 합니다. 그러나 pLSI는 온전한 확률모형을 도입하지 못하였고 이를 보완한 LDA가 2003년에 제시됩니다.
LDA가 토픽모델링의 기원이 아님에도 온전한 배경을 가진 첫 모형이기 때문에 사실상 표준으로 자리잡고, 가장 널리 사용됩니다. LDA 이후에도 HDP, TOT, AT, ATOT 등 다양한 모형들이 제시되었으나 대부분 LDA를 기반으로 확장한 모형입니다.
Latent dirichlet allocation
Generative process
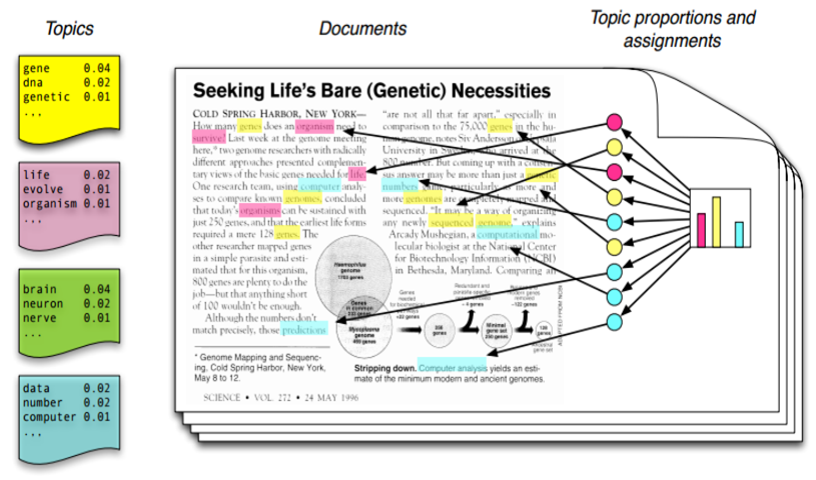
LDA는 문서에 대하여 확률적 생성모형(Generative model)을 가정합니다. LDA의 고안자인 Blei가 논문에 실은 아래 그림은 LDA에서 가정하고 있는 생성모형을 나타내는 그림입니다.
토픽에 대한 확률적인 단어분포가 있다고 가정합시다. 예를들어 유전자에 관한 토픽이 있다면 DNA, Gene 등의 단어들이 높은 확률로 포함되어 있을것입니다. Computer등의 단어도 포함될 수 있지만 확률값은 낮겠죠?
우리가 빈 종이에 글을 쓴다고 합시다. 사전에 가정한 많은 토픽들 중에서 어떤 토픽을 하나 고르고 토픽에 해당하는 단어를 하나 고릅니다. 최종적으로 선택된 단어를 빈종이에 추가합니다. 이와같은 과정을 반복하면 하나의 문서가 완성됩니다.
물론 여기서 하나의 가정이 더 필요합니다.
눈치 채셨을수도 있지만, 사람이 쓰는 글에는 문맥이라는것이 있습니다. 어떤 단어가 등장하는지도 중요하지만, 어떤 순서로 등장하는지도 중요합니다. “사과는 빨갛고 바나나는 노랗다”는 말이 되지만 “사과는 노랗고 바나나는 빨갛다” 혹은 “사과는 바나나는 빨갛다 노랗고”는 조금 이상하지요. 그러나 LDA모형의 생성모형에서는 세 문장을 구분할 수 없습니다. 이를 Bag-of-Words 라고 하는데, 말그대로 문서를 단어의 Bag으로 본다는 가정입니다.
Bag이기 때문에 순서는 관계없고 어떤 단어가 등장했느냐가 중요합니다. 물론 현실적이지는 않고 저자들도 알고 있으나 당시로써는 어쩔 수 없었던 것으로 보입니다. 요즘 뜨고있는 Deep learning을 이용하면 해결할수 있지 않을까 싶기는 한데, 뭐 일단은 그렇습니다.
다시 생성모형으로 돌아가 봅시다. LDA의 생성모형에 따르면 어떤 문서 안에 있는 각 단어는 K개의 토픽중에 하나를 고르고, V개의 단어 중에서 선택된 토픽의 단어분포에 따라 하나를 고르는 과정의 반복으로 만들어 졌습니다. 즉 우리가 가지고 있는 문서-단어 행렬은 문서-토픽분포와 토픽-단어분포를 이용하여 생성된 것으로 볼 수 있습니다(단순 곱은 아닙니다). 그렇다면 문서-단어 행렬을 이용하여 문서-토픽분포와 토픽-단어분포를 추정하는것도 가능하겠지요. 그리고 데이터에 기반하여 미지의 확률값을 추정하기 위해서 우리는 Bayesian rule을 사용할 수 있습니다. 이것이 LDA Topic modeling입니다.
덧붙이자면 문서의 생성과정에서 K개 토픽중에 하나를 고르는 과정은 다항분포(Multinomial distribution)로 모델링 할 수 있습니다. V개 단어중에 하나를 고르는 과정도 마찬가지로 다항분포입니다.
그럼 다항분포에서 각 클래스가 선택될 확률은 어떻게 정의할 수 있을까요?
다항분포의 결레 사전분포(Conjugate prior)는 Dirichlet distribution입니다. LDA의 D가 여기서 나온 것을 알 수 있습니다.
Posterior inference
앞에서 설명한 것과 같이 LDA는 베이지안에 기반한 방법이고, 베이지안의 핵심은 사후확률분포를 추론(Posterior inference)하는 것 입니다.
따라서 LDA의 핵심 역시 각 문서의 단어들이 어떤 토픽에서 추출되었는지(z)와 문서-토픽 분포(theta)와 토픽-단어 분포(phi)를 추론하는 것으로 생각할 수 있습니다.
이를 위한 몇가지 추론 방법들이 있습니다. 대표적으로 LDA의 원래 논문에서는 Variational inference라고 해서 Kullback–Leibler divergence를 이용한 방법이 있습니다. 또 널리 사용되는 방법중에 Gibbs sampling을 이용한 방법도 있는데, 본 글에서는 Gibbs sampling을 설명하고 Gibbs sampling을 이용한 LDA를 구현하도록 하겠습니다.
Gibbs sampling
추론의 대상인 사후분포가 많은 모수들의 결합확률분포로 표현될 경우, Closed form을 찾기 어려운 경우가 많습니다. 이때 사용할 수 있는 방법이 Gibbs sampling입니다.
사후분포를 추정할 때, N개의 모수가 있다고 하면 N개의 모수를 가진 결합확률분포를 추정하기는 어렵습니다. 대신 N-1개의 모수를 고정시키면 사후분포는 모수가 1개인 분포가 됩니다. N-1개의 모수를 고정시키고 1개의 모수에 대해서만 추정하는 과정을 N번 반복하고, 이 전체 과정을 여러번 반복하여 사후분포를 추정하는 것이 Gibbs sampling입니다. Gibbs sampling의 반복횟수가 충분할 경우 추정되는 사후분포는 실제 분포에 수렴한다고 합니다.
LDA에 Gibbs sampling을 적용할 경우 파라미터는 다음과 같이 추정될 수 있습니다 (자세한 과정은 참고문헌에 Darling의 논문을 참고 바랍니다).
z는 각 문서의 단어들이 어떤 토픽에서 추출되었는지를 나타내는 변수입니다. 위에서 LDA는 각 문서의 단어들이 어떤 토픽에서 추출되었는지(z)와 문서-토픽 분포(theta)와 토픽-단어 분포(phi)를 추론하는것이라고 했는데, theta와 phi가 빠진 이유는, z를 알 경우 z를 통해서 theta와 phi를 계산할 수 있기 때문입니다.
위 식에서 제일 마지막을 보면 alpha와 beta는 문서-토픽 분포와 토픽-단어 분포를 구하는데 사용되는 Parameter입니다. 두 값이 커질수록 문서-토픽분포(alpha)와 토픽-단어분포(beta)의 쏠림이 적어지게 됩니다(Bias가 줄어들고 Regulerize 된다고 표현하고 싶은데 통계적으로 맞는 표현인지 잘 모르겠습니다).
어쨋든 놀랍지 않나요? Gibbs sampling을 통해 LDA의 사후분포 추론이 단순히 빈도를 세는(Count)문제로 변환되었습니다!! 문제 자체가 쉬워졌고 구현도 간단하기 때문에 Gibbs sampling을 이용한 LDA가 널리 사용됩니다.
그리고 추가적으로, LDA에 Gibbs sampling을 적용하여 전개하다보면 적분으로 몇몇 변수들이 사라집니다. 이렇게 몇몇 변수들이 사라진 채로 진행되는 Gibbs sampling을 Collapsed gibbs sampling이라고 합니다.
Algorithm
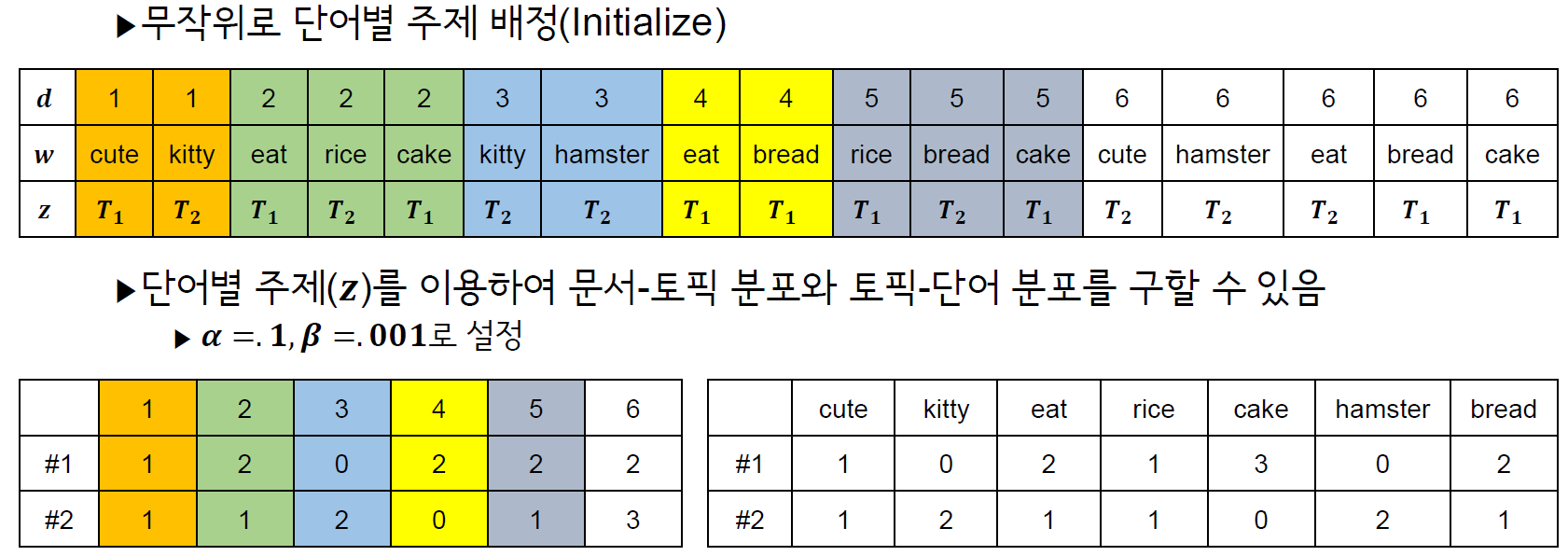
Gibbs sampling을 사용한 LDA 과정은 다음과 같습니다. 한눈에 봐도 굉장히 짧고 단순한 것을 알 수 있습니다.
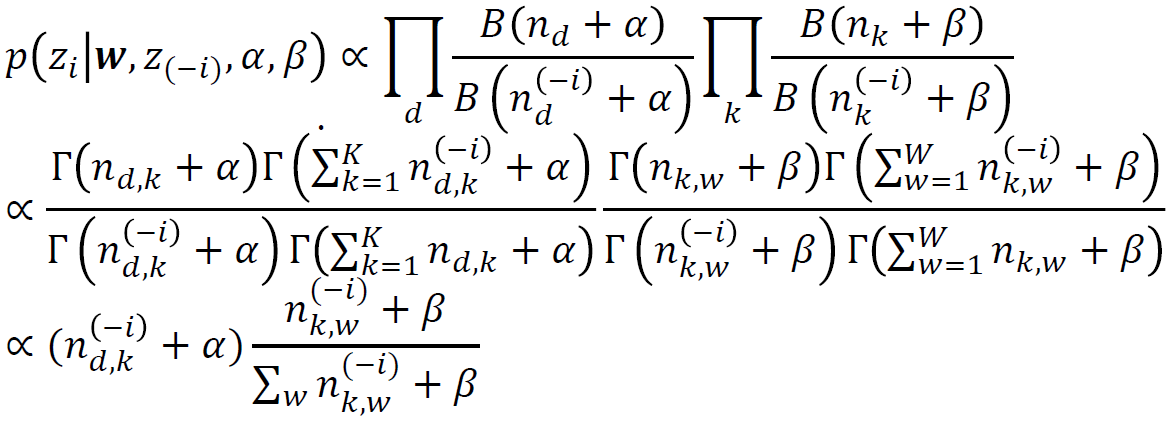
다만 한눈에 감이 안오실 수도 있는데, 아래 예제를 따라가다 보면 이해가 쉬우실 것 같습니다 (bab2min님 블로그에 있는 예제에서 식을 Darling의 것으로 수정하였고 다시 작성하였습니다, 식이 변경되었지만 어차피 비례식이라 결과는 같습니다).
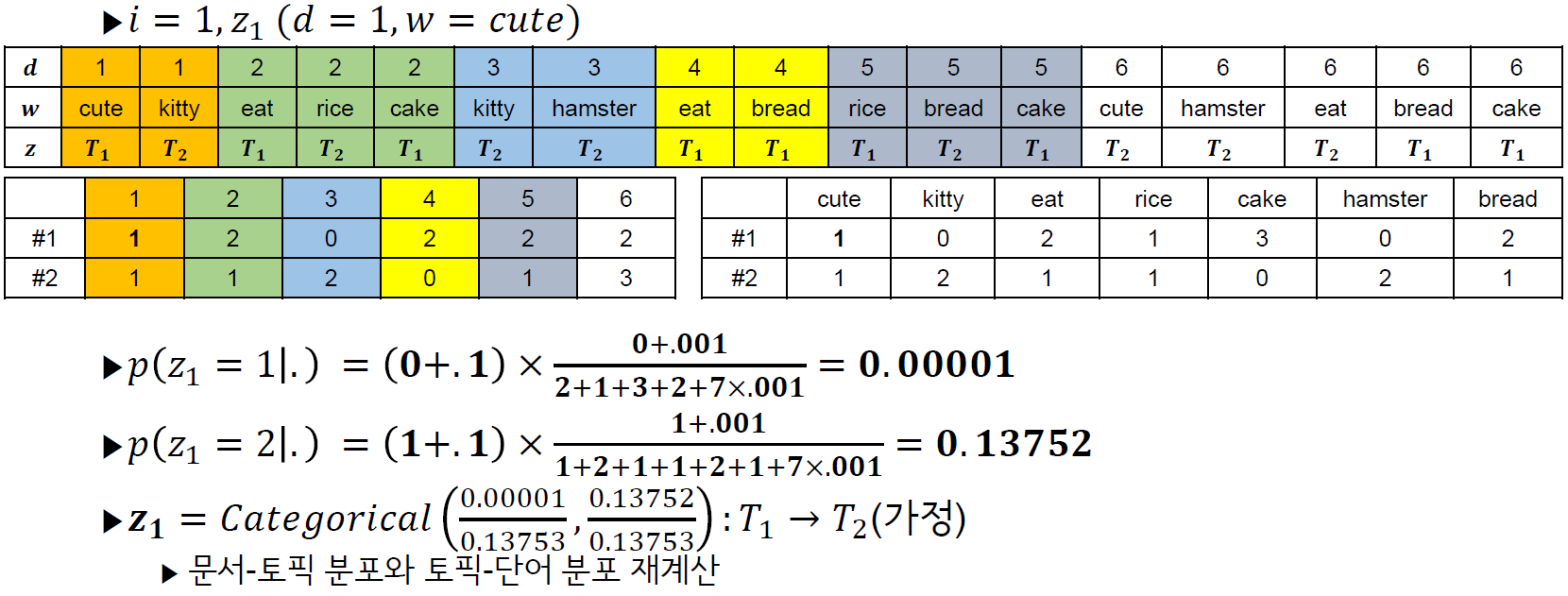
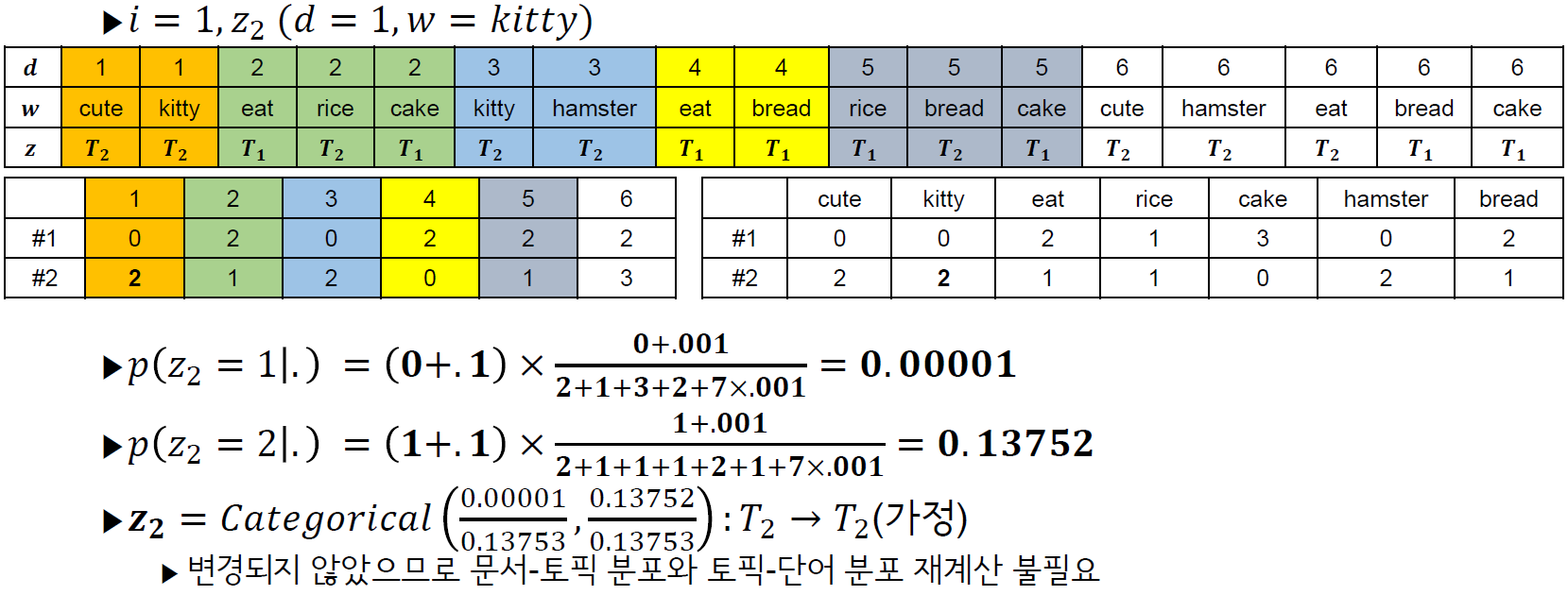위에서는 z_2까지만 하였는데, z전체에 대하여 위 과정을 반복하면 1회의 Gibbs sampling이 완료되는 것 입니다.
Code in R
위의 알고리즘을 R로 구현해보겠습니다. 우선 아래와 같이 6개의 문서가 있다고 가정 하겠습니다(bab2min님 블로그의 예제를 따라했음을 밝힙니다).
문서를 단어단위로 자르고…
rawdocs = c('cute kitty',
'eat rice cake',
'kitty hamster',
'eat bread',
'rice bread cake',
'cute hamster eat bread cake')
docs = strsplit(rawdocs, split=' ')
print(docs)
[[1]]
[1] "cute" "kitty"
[[2]]
[1] "eat" "rice" "cake"
[[3]]
[1] "kitty" "hamster"
[[4]]
[1] "eat" "bread"
[[5]]
[1] "rice" "bread" "cake"
[[6]]
[1] "cute" "hamster" "eat" "bread" "cake"
어휘집을 만들고, 문서 내의 단어들을 어휘집읜 index로 바꿔주는 등의 기본적인 전처리를 합니다.
문서가 숫자로 바뀌었네요.
vocab = unique(unlist(docs))
for(i in 1:length(docs)) {
docs[[i]] = match(docs[[i]], vocab)
}
print(vocab)
print(docs)
[1] "cute" "kitty" "eat" "rice" "cake" "hamster" "bread"
[[1]]
[1] 1 2
[[2]]
[1] 3 4 5
[[3]]
[1] 2 6
[[4]]
[1] 3 7
[[5]]
[1] 4 7 5
[[6]]
[1] 1 6 3 7 5
모형을 위한 파라미터를 설정합니다. 각 파라미터에 대한 설명은 다음과 같습니다.
- K: 토픽 수
- alpha: 문서-토픽분포의 결정을 위한 Hyper-parameter(작을수록 적은수의 토픽으로 쏠림)
- beta: 토픽-단어분포의 결정을 위한 Hyper-parameter(작을수록 적은수의 단어로 쏠림)
- iter.max: Gibbs sampling 반복 횟수
하이퍼파라미터인 만큼 이들을 정하는데 정확한 방법은 없습니다. 다만 토픽수같은 경우 Perplexity라는 지표를 계산해서 정하는게 일반적입니다.
K = 2
alpha = .1
beta = .001
iter.max = 1000
아래 식은 z에서 문서-토픽분포와 토픽-단어분포를 계산할 수 있는 함수입니다. Gibbs sampling 과정에서 반복해서 사용하게 되니 함수로 만들어 놓겠습니다.
func.document_topic = function(topic_assign, K, document_topic){
document_topic = document_topic*0
for(doc in 1:length(topic_assign)){
for(topic in 1:K){
document_topic[doc,topic] = sum(topic_assign[[doc]]==topic)
}
}
return(document_topic)
}
func.topic_word = function(topic_assign, docs, topic_word){
topic_word = topic_word*0
for(doc in 1:length(docs)){
for(word in 1:length(docs[[doc]])){
topic_index = topic_assign[[doc]][word]
word_index = docs[[doc]][word]
topic_word[topic_index,word_index] = topic_word[topic_index,word_index]+1 # word-topic count matrix 업데이트
}
}
return(topic_word)
}
z를 임의로 할당해 놓습니다. 임의로 할당되었기 때문에 현재로써는 아무런 의미가 없지만, 추후 gibbs sampling을 통해 최적화 될 것입니다.
topic_assign = sapply(docs, function(x) sample(1:K, length(x), replace=TRUE))
topic_word = matrix(0, K, length(vocab)) # 주제별 단어분포(word_topic) 초기화
topic_word = func.topic_word(topic_assign,docs,topic_word)
document_topic = matrix(0, length(docs), K) # 문서-토픽분포 초기화
document_topic = func.document_topic(topic_assign,K,document_topic)
print(topic_assign) # 임의로 할당된 개별 문서의 단어별 주제 분포
print(topic_word) # 주제별 단어분포
print(document_topic) # 문서별 주제분포
[[1]]
[1] 1 1
[[2]]
[1] 2 2 2
[[3]]
[1] 1 1
[[4]]
[1] 2 2
[[5]]
[1] 2 2 2
[[6]]
[1] 1 1 2 2 2
[,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 2 2 0 0 0 2 0
[2,] 0 0 3 2 3 0 3
[,1] [,2]
[1,] 2 0
[2,] 0 3
[3,] 2 0
[4,] 0 2
[5,] 0 3
[6,] 2 3
이 아래가 Gibbs sampling을 이용한 LDA 알고리즘입니다. 출력된 값을 보면 1000회 반복을 시켰지만, 어느정도 반복 뒤에는 변화가 없는것을 보실 수 있습니다.
for(iter in 1:iter.max){
for(doc in 1:length(docs)){
for(word in 1:length(docs[[doc]])){
z.old = topic_assign[[doc]][word] # 그 단어의 이전 z
w.index = docs[[doc]][word] # 해당 단어의 index
# 두 분포에서 이전 z 관련 정보를 제거
document_topic[doc, z.old] = document_topic[doc, z.old] - 1
topic_word[z.old, w.index] = topic_word[z.old, w.index] - 1
prob_topic = rep(0, K)
for(k in 1:K){
prob_topic[k] = (document_topic[doc, k] + alpha)*(topic_word[k, w.index]+beta)/rowSums(topic_word+beta)[k]
}
# prob_topic = prob_topic/sum(prob_topic)
z.new = sample(1:K, 1, prob=prob_topic) # sample함수의 prop 파라미터는 내부적으로 정규화
if(z.new != z.old){
print(paste0('doc:', doc, ' token:', word, ' topic:',z.old,'=>',z.new))
topic_assign[[doc]][word] = z.new
}
topic_word = func.topic_word(topic_assign, docs, topic_word)
document_topic = func.document_topic(topic_assign, K, document_topic)
}
}
}
[1] "doc:1 token:1 topic:1=>2"
[1] "doc:1 token:2 topic:2=>1"
[1] "doc:2 token:3 topic:1=>2"
[1] "doc:4 token:1 topic:2=>1"
[1] "doc:2 token:1 topic:2=>1"
[1] "doc:5 token:2 topic:1=>2"
[1] "doc:4 token:2 topic:1=>2"
[1] "doc:6 token:4 topic:1=>2"
[1] "doc:4 token:1 topic:1=>2"
[1] "doc:6 token:3 topic:1=>2"
[1] "doc:2 token:1 topic:1=>2"
[1] "doc:1 token:1 topic:2=>1"
[1] "doc:6 token:1 topic:2=>1"
[1] "doc:6 token:1 topic:1=>2"
[1] "doc:1 token:1 topic:1=>2"
[1] "doc:6 token:1 topic:2=>1"
[1] "doc:1 token:1 topic:2=>1"
[1] "doc:6 token:2 topic:1=>2"
[1] "doc:3 token:2 topic:1=>2"
[1] "doc:3 token:2 topic:2=>1"
[1] "doc:6 token:2 topic:2=>1"
[1] "doc:6 token:1 topic:1=>2"
[1] "doc:6 token:1 topic:2=>1"
[1] "doc:6 token:4 topic:2=>1"
[1] "doc:6 token:4 topic:1=>2"
추정된 문서-토픽분포와 토픽-단어 분포를 확률분포로 변경하는 것은 아래와 같은 방법으로 가능합니다.
문서와 단어들을 보시면 잘 분리된 것을 보실 수 있습니다.
theta = (document_topic + alpha) / rowSums(document_topic + alpha)
print(theta)
phi = (topic_word + beta) / rowSums(topic_word + beta)
colnames(phi) = vocab
print(phi)
[,1] [,2]
[1,] 0.95454545 0.04545455
[2,] 0.03125000 0.96875000
[3,] 0.95454545 0.04545455
[4,] 0.04545455 0.95454545
[5,] 0.03125000 0.96875000
[6,] 0.40384615 0.59615385
cute kitty eat rice cake hamster bread
[1,] 3.331114e-01 3.331114e-01 0.0001664724 0.0001664724 0.0001664724 3.331114e-01 0.0001664724
[2,] 9.085128e-05 9.085128e-05 0.2726446807 0.1817934042 0.2726446807 9.085128e-05 0.2726446807
References
- Blei, David M., Andrew Y. Ng, and Michael I. Jordan. “Latent dirichlet allocation.” Journal of machine Learning research 3.Jan (2003): 993-1022.
- Darling, William M. “A theoretical and practical implementation tutorial on topic modeling and gibbs sampling.” Proceedings of the 49th annual meeting of the association for computational linguistics: Human language technologies. 2011.
- https://ethen8181.github.io/machine-learning/clustering_old/topic_model/LDA.html
- https://bab2min.tistory.com/569