2018 Spring Data Analytics @Dept. of Industrial engineering
Dimension reduction
Contents
- Principal component analysis (PCA)
- Truncated singular value decomposition and latent semantic analysis
- Non-negative matrix factorization (NMF or NNMF)
- Latent Dirichlet Allocation (LDA)
- Another dimension reduction method for Visualization
Used library
- Sci-kit learn: Machine learning을 Python에서 손쉽게 이용할 수 있도록 작성된 라이브러리, 전처리/모형구축/평가 등 전 과정에 관련한 모듈등이 구축되어 있음 (http://scikit-learn.org)
- Matplotlib: Python에서 Plot을 그릴때 가징 기본적인 라이브러리, 본 예제에서는 PCA등을 이용하여 차원축소된 데이터를 시각화 하는데 사용 (https://matplotlib.org/)
import matplotlib.pyplot as plt
Sample data
샘플데이터는 Sci-kit learn에 포함되어있는 20 Newsgroups data를 사용
- 20 Newsgroups data: The 20 Newsgroups data set is a collection of approximately 20,000 newsgroup documents, partitioned (nearly) evenly across 20 different newsgroups (http://qwone.com/~jason/20Newsgroups/).
from sklearn.datasets import fetch_20newsgroups
news = fetch_20newsgroups(shuffle=True, random_state=777, remove=('headers', 'footers', 'quotes'))
print('-'*20 + '20 Newsgroups data class' + '-'*20)
print(news.target_names)
print('-'*20 + '20 Newsgroups data sample' + '-'*20)
print(news.data[0])
--------------------20 Newsgroups data class--------------------
['alt.atheism', 'comp.graphics', 'comp.os.ms-windows.misc', 'comp.sys.ibm.pc.hardware', 'comp.sys.mac.hardware', 'comp.windows.x', 'misc.forsale', 'rec.autos', 'rec.motorcycles', 'rec.sport.baseball', 'rec.sport.hockey', 'sci.crypt', 'sci.electronics', 'sci.med', 'sci.space', 'soc.religion.christian', 'talk.politics.guns', 'talk.politics.mideast', 'talk.politics.misc', 'talk.religion.misc']
--------------------20 Newsgroups data sample--------------------
And I recommend the movie _The Thin Blue Line_, which is about the
same case. Not as much legal detail, but still an excellent film. It
shows how very easy it is to come up with seemingly conclusive
evidence against someone whom you think is guilty.
Pre-processing
from sklearn.feature_extraction.text import TfidfVectorizer
data_samples = news.data[:1000]
data_target = news.target[:1000]
data_class = news.target_names
tfidf_vectorizer = TfidfVectorizer(max_df=0.95, min_df=2, max_features=100, stop_words='english')
TFIDF = tfidf_vectorizer.fit_transform(data_samples)
print(TFIDF.toarray()[0:2])
[[0. 0. 0. 0. 0. 0.
0. 0. 0. 0.61061632 0. 0.
0.61941575 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0.49342866 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 0.
0.34064892 0. 0. 0. 0.77129062 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0.31703364 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0.32037793 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0.29311558 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. ]]
Principal component analysis (PCA)
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(TFIDF.toarray())
print('-'*20 + 'Explained variance ratio' + '-'*20)
print(pca.explained_variance_ratio_)
print('-'*20 + 'Singular value' + '-'*20)
print(pca.singular_values_)
--------------------Explained variance ratio--------------------
[0.03153768 0.02615567]
--------------------Singular value--------------------
[5.1851592 4.72204602]
import matplotlib.cm as cm
import numpy as np
PCA_TFIDF = pca.transform(TFIDF.toarray())
print(PCA_TFIDF.shape)
plt.figure(figsize=(10,10))
plt.scatter(PCA_TFIDF[:,0], PCA_TFIDF[:,1], c=data_target)
plt.show()
(1000, 2)
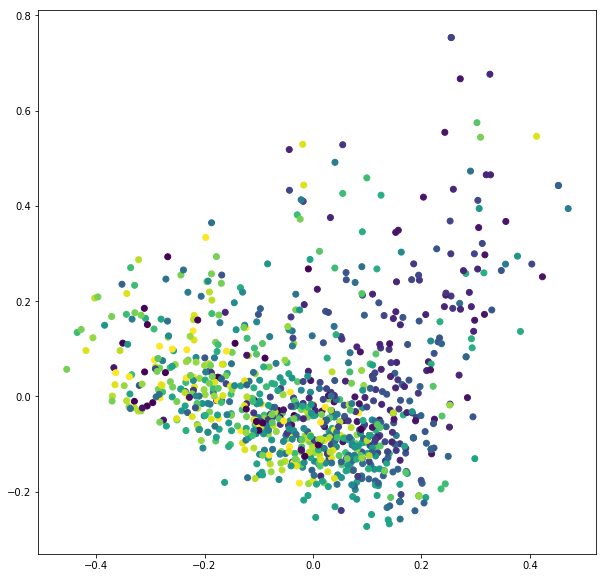
Best example of PCA
Iris data set(https://en.wikipedia.org/wiki/Iris_flower_data_set)
- Feature: the length and the width of the sepals and petals (4 features)
- Class: Iris setosa, Iris virginica and Iris versicolor
from sklearn.datasets import load_iris
IRIS = load_iris()
X = IRIS.data
y = IRIS.target
target_names = IRIS.target_names
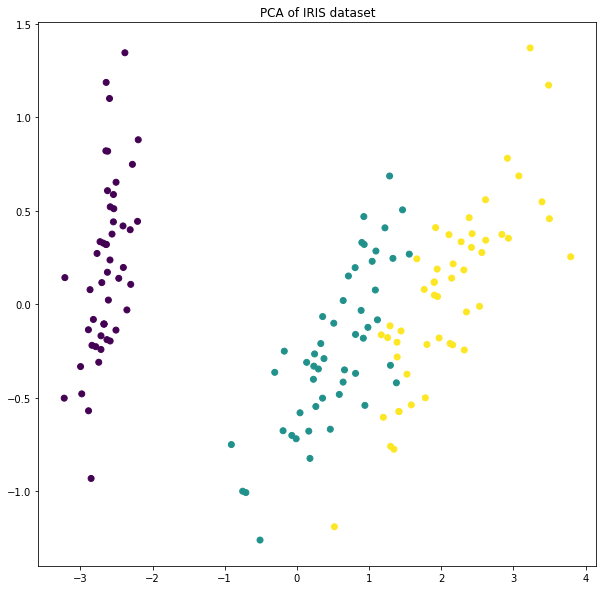
pca_iris = PCA(n_components=2)
PCA_IRIS = pca_iris.fit(X).transform(X)
print('-'*20 + 'Explained variance ratio' + '-'*20)
print(pca_iris.explained_variance_ratio_)
print('-'*20 + 'Singular value' + '-'*20)
print(pca_iris.singular_values_)
plt.figure(figsize=(10,10))
plt.scatter(PCA_IRIS[:,0], PCA_IRIS[:,1], c=y)
plt.title('PCA of IRIS dataset')
plt.show()
--------------------Explained variance ratio--------------------
[0.92461621 0.05301557]
--------------------Singular value--------------------
[25.08986398 6.00785254]
Singular value decomposition (SVD) and Latent semantic analysis (LSA)
from sklearn.decomposition import TruncatedSVD
svd = TruncatedSVD(n_components=10, algorithm='randomized', n_iter=5, random_state=None, tol=0.0)
SVD_TFIDF = svd.fit(TFIDF)
print("Topics in SVD(LSA) model:")
feature_names = tfidf_vectorizer.get_feature_names()
for topic_idx, topic in enumerate(svd.components_):
message = "Topic #%d: " % topic_idx
message += ", ".join([feature_names[i] for i in topic.argsort()[:-10 -1:-1]])
print(message)
Topics in SVD(LSA) model:
Topic #0: just, don, like, know, people, think, does, time, good, use
Topic #1: thanks, mail, windows, does, know, help, edu, program, used, use
Topic #2: know, does, people, thanks, god, think, believe, did, say, mean
Topic #3: just, know, right, mail, edu, way, thanks, does, key, really
Topic #4: edu, think, good, don, mail, right, let, com, thanks, know
Topic #5: good, just, ve, seen, time, does, game, know, didn, really
Topic #6: think, like, don, did, know, need, drive, game, make, windows
Topic #7: edu, like, god, ve, seen, new, people, things, believe, say
Topic #8: ve, use, seen, don, know, used, people, got, just, case
Topic #9: com, ve, drive, think, thanks, god, seen, did, used, bit
print(svd.components_.shape)
print(TFIDF.shape)
(10, 100)
(1000, 100)
Image compression with SVD (with numpy)
import numpy as np
from PIL import Image
# 이미지 로딩
img = Image.open("sorry_nephew.jpg")
imggray = img.convert('LA')
# 이미지 벡터화
imgmat = np.array(list(imggray.getdata(band=0)), float)
imgmat.shape = (imggray.size[1], imggray.size[0])
imgmat = np.matrix(imgmat)
# 원본이미지 출력
plt.figure(figsize=(5,5))
fig_ori=plt.imshow(imgmat, cmap='gray')
fig_ori.axes.get_xaxis().set_visible(False)
fig_ori.axes.get_yaxis().set_visible(False)

# SVD
U, sigma, V = np.linalg.svd(imgmat)
# 특이값 개수별 이미지 재구성
plt.figure(figsize=(10,10))
for i in range(1, 10):
reconstimg = np.matrix(U[:, :i*5]) * np.diag(sigma[:i*5]) * np.matrix(V[:i*5, :])
plt.subplot("33{i}".format(i=i))
fig = plt.imshow(reconstimg, cmap='gray')
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
plt.title("n = {i}".format(i=(i*5)))
plt.show()

Non-negative matrix factorization (NMF)
from sklearn.decomposition import NMF
nmf = NMF(n_components=10, random_state=1, beta_loss='kullback-leibler', solver='mu', max_iter=1000, alpha=.1, l1_ratio=.5)
NMT_TFIDF = nmf.fit(TFIDF)
print("Topics in NMF model (generalized Kullback-Leibler divergence):")
feature_names = tfidf_vectorizer.get_feature_names()
for topic_idx, topic in enumerate(nmf.components_):
message = "Topic #%d: " % topic_idx
message += ", ".join([feature_names[i] for i in topic.argsort()[:-10 -1:-1]])
print(message)
Topics in NMF model (generalized Kullback-Leibler divergence):
Topic #0: make, say, like, way, don, want, does, true, really, problem
Topic #1: thanks, does, mail, help, windows, know, program, file, need, set
Topic #2: new, year, probably, key, need, line, years, 10, number, information
Topic #3: just, right, know, way, mean, really, tell, used, doesn, mail
Topic #4: think, don, edu, did, want, public, let, going, know, case
Topic #5: good, time, didn, better, point, game, long, great, just, order
Topic #6: people, time, believe, god, fact, come, government, world, point, read
Topic #7: like, come, question, number, different, things, tell, high, believe, seen
Topic #8: use, ve, used, using, don, available, fact, thing, got, point
Topic #9: drive, work, seen, com, problems, hard, bit, read, got, ve
Latent Dirichlet Allocation (LDA)
from sklearn.decomposition import LatentDirichletAllocation
lda = LatentDirichletAllocation(n_components=10, random_state=777, verbose=0, learning_method='batch', max_iter=200)
lda.fit(TFIDF)
print("Topics in LDA model:")
feature_names = tfidf_vectorizer.get_feature_names()
for topic_idx, topic in enumerate(lda.components_):
message = "Topic #%d: " % topic_idx
message += ", ".join([feature_names[i] for i in topic.argsort()[:-10 -1:-1]])
print(message)
Topics in LDA model:
Topic #0: drive, chip, hard, set, believe, problems, look, problem, question, think
Topic #1: game, time, think, just, right, don, great, like, fact, said
Topic #2: line, 10, year, did, years, 12, ll, didn, let, dod
Topic #3: edu, mail, list, make, space, different, thanks, tell, order, word
Topic #4: good, number, case, like, following, given, government, tape, ve, come
Topic #5: thanks, does, windows, ve, seen, know, file, like, help, work
Topic #6: people, god, really, just, don, say, think, know, time, does
Topic #7: com, key, new, data, information, read, used, just, great, bit
Topic #8: used, use, program, high, want, son, like, probably, using, help
Topic #9: public, doesn, going, don, real, mean, way, better, know, problem
Visualzing the LDA models with pyLDAvis
import pyLDAvis
import pyLDAvis.sklearn
pyLDAvis.enable_notebook()
pyLDAvis.sklearn.prepare(lda, TFIDF, tfidf_vectorizer)
Another dimension reduction method for Visualization
데이터 시각화를 위한 차원축소 방법들
- t-distributed Stochastic Neighbor Embedding (https://en.wikipedia.org/wiki/T-distributed_stochastic_neighbor_embedding)
- Multidimensional scaling (https://en.wikipedia.org/wiki/Multidimensional_scaling)
- Isomap (https://en.wikipedia.org/wiki/Isomap)
- Locally Linear Embedding (https://en.wikipedia.org/wiki/Nonlinear_dimensionality_reduction#Locally-linear_embedding)
더 알아보기: https://en.wikipedia.org/wiki/Nonlinear_dimensionality_reduction
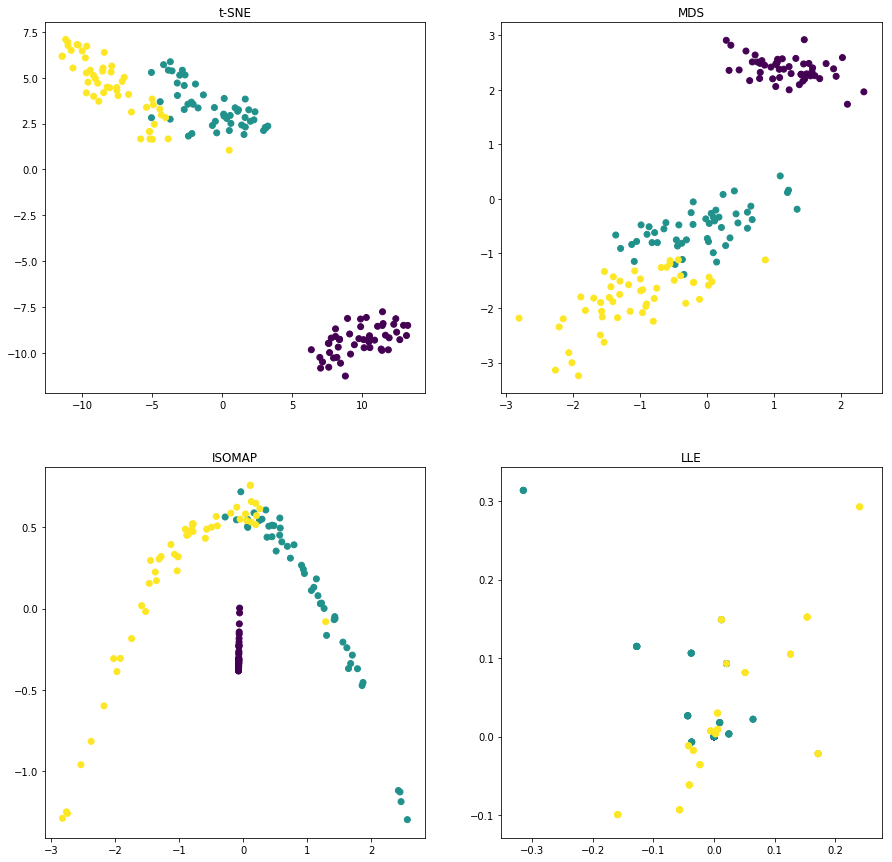
from sklearn.manifold import TSNE, MDS, Isomap, LocallyLinearEmbedding, SpectralEmbedding
TSNE_IRIS = TSNE(n_components=2, learning_rate=1.0, n_iter=750).fit_transform(X)
MDS_IRIS = MDS(n_components=2, dissimilarity='euclidean').fit_transform(X)
ISOMAP_IRIS = Isomap(n_neighbors=10, n_components=2).fit_transform(X)
LLE_IRIS = LocallyLinearEmbedding(n_neighbors=1, n_components=2).fit_transform(X)
plt.figure(figsize=(15,15))
plt.subplot(221)
plt.title("t-SNE")
plt.scatter(TSNE_IRIS[:,0], TSNE_IRIS[:,1], c=y)
plt.subplot(222)
plt.title("MDS")
plt.scatter(MDS_IRIS[:,0], MDS_IRIS[:,1], c=y)
plt.subplot(223)
plt.title("ISOMAP")
plt.scatter(ISOMAP_IRIS[:,0], ISOMAP_IRIS[:,1], c=y)
plt.subplot(224)
plt.title("LLE")
plt.scatter(LLE_IRIS[:,0], LLE_IRIS[:,1], c=y)
plt.show()