서론

시계열 분석(Time series analysis)이란,
독립변수(Independent variable)를 이용하여 종속변수(Dependent variable)를 예측하는 일반적인 기계학습 방법론에 대하여 시간을 독립변수로 사용한다는 특징이 있다. 독립변수로 시간을 사용하는 특성때문에 분석에 있어서 일반적인 방법론들과는 다른 몇가지 고려가 필요하다.

본 포스트에서는 시계열 분석(혹은 예측)에 있어서 가장 널리 사용되는 모델중 하나인 ARIMA에 대해 알아보고 Python을 통해 구현해본다.
본 포스트에서는

ARIMA의 간단한 개념
ARIMA 모델의 파라미터 선정 방법
실제 데이터와 ARIMA 모델을 이용한 미래 예측

등 과 관련된 내용을 다룬다.

ARIMA(Autoregressive Integrated Moving Average)

ARIMA는 Autoregressive Integrated Moving Average의 약자로, Autoregressive는 자기회귀모형을 의미하고, Moving Average는 이동평균모형을 의미한다.

즉, ARIMA는 자기회귀와 이동평균을 둘 다 고려하는 모형인데, ARMA와 ARIMA의 차이점은 ARIMA의 경우 시계열의 비정상성(Non-stationary)을 설명하기 위해 관측치간의 차분(Diffrance)을 사용한다는 차이점이 있다.
ARMA와 ARIMA 외에도 ARIMAX 등의 방법도 있는데, 이는 본 포스트에서 살펴보지 않는다.

AR: 자기회귀(Autoregression). 이전 관측값의 오차항이 이후 관측값에 영향을 주는 모형이다. 아래 식은 제일 기본적인 AR(1) 식으로, theta는 자기상관계수, epsilon은 white noise이다. Time lag은 1이 될수도 있고 그 이상이 될 수도 있다.
$eq_ar1$
I: Intgrated. 누적을 의미하는 것으로, 차분을 이용하는 시계열모형들에 붙이는 표현이라고 생각하면 편하다.
MA: 이동평균(Moving Average). 관측값이 이전의 연속적인 오차항의 영향을 받는다는 모형이다. 아래 식은 가장 기본적인 MA(1) 모형을 나타낸 식으로, beta는 이동평균계수, epsilon은 t시점의 오차항이다.
$eq_ma1$

현실에 존재하는 시계열자료는 불안정(Non-stationary)한 경우가 많다. 그런데 AR(p), MA(q) 모형이나, 이 둘을 합한 ARMA(p, q)모형으로는 이러한 불안정성을 설명할 수가 없다.
따라서 모형 그 자체에 이러한 비정상성을 제거하는 과정을 포함한것이 ARIMA모형이며 ARIMA(p, d, q)로 표현한다.
$eq_arima$

$eq_arima_mu$
$eq_arima_ar$
$eq_arima_ma$
$eq_arima_d0$
$eq_arima_d1$
$eq_arima_d2$

위와 같은 특징에 따라 ARMIA(p, d, q)는 AR, MA, ARMA를 모두 표현할 수 있다.

AR(p) = ARIMA(p, 0, 0)
MA(q) = ARIMA(0, 0, q)
ARMA(p, q) = ARIMA(p, 0, q)

이 외에도 ARIMA와 관련한 많은 내용이 있으나, 본 포스트에서는 생략하고 이후 포스트 진행에 필요한 부분들이 있으면 간략하게 설명하겠다. 참고할만한 서적으로는 ARIMA를 포함하여 통계적 시계열분석의 Standard라고 할 수 있는 Box, George; Jenkins, Gwilym (1970). Time Series Analysis: Forecasting and Control.(아마존 링크)를 참조하시면 좋을 듯 하다.

데이터

본 포스트에서 ARIMA를 이용한 예측에 사용할 데이터는 Blockchain Luxembourg S.A에서 Export한 최근 60일간의 비트코인 시세와 관련된 자료이다.
CSV파일로 Export했으며, Column name만 수동으로 추가하여주었다.

Date Price

2017-10-12 5325.130683333333

2017-10-13 5563.806566666666

2017-10-14 5739.438733333333

… …

Date	Price
2017-10-12	5325.130683333333
2017-10-13	5563.806566666666
2017-10-14	5739.438733333333
…	…

미화(USD)기준 가격 변동임에도, 며칠전 일련의 사태(비트코인 플래티넘 등)로 폭등했던 흔적이 남아있다.
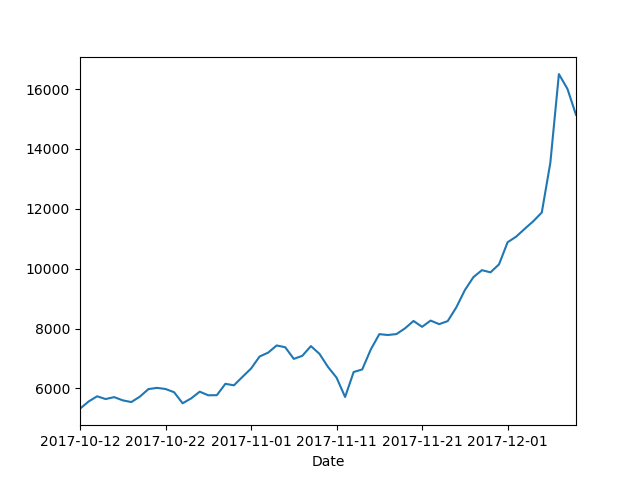
rawdata_plot

import pandas as pd

series = pd.read_csv('market-price.csv', header=0, index_col=0, squeeze=True)
series.plot()

ARIMA 모수 설정

ARIMA의 모수는 크게 3가지가 있다. AR모형의 Lag을 의미하는 p, MA모형의 Lag을 의미하는 q, 차분(Diffrence)횟수를 의미하는 d 가 그것이다. 보통은 p, d, q의 순서로 쓴다.
통상적으로 p + q < 2, p * q = 0 인 값들을 많이 사용한다.

여기서 p * q = 0 이라 하면, 두 값중 하나는 0이라는 이야기이다. ARIMA는 AR모형과 MA모형을 하나로 합쳤다면서 둘 중 하나의 모수가 0인건 또 무슨소리? 라고 할지 모르겠지만, 실제로 대부분의 시계열 자료에서는 하나의 경향만을 강하게 띄기 때문에, 이렇게 사용하는것이 더 잘 맞는다고 한다.

그렇다면, p와 d, q는 어떻게 정해야 할까? Rules of thumb이긴 하지만 ACF plot와 PACF plot을 통해 AR 및 MA의 모수를 추정할 수 있다.

ACF(Autocorrelation function) : Lag에 따른 관측치들 사이의 관련성을 측정하는 함수
$eq_acf$
PACF(Partial autocorrelation function) : k 이외의 모든 다른 시점 관측치의 영향력을 배제하고 $eq_yt$ 와 $eq_ytk$ 두 관측치의 관련성을 측정하는 함수
$eq_pacf$

시계열 데이터가 AR의 특성을 띄는 경우, ACF는 천천히 감소하고 PACF는 처음 시차를 제외하고 급격히 감소한다.
반대로, MA의 특성을 띄는 경우 ACF는 급격히 감소하고 PACF는 천천히 감소한다.
급격히 감소하는 시차를 각 AR과 MA 모형의 모수(p, q)로 사용할 수 있다. 또한 데이터를 차분하여 ACF 및 PACF 계산함으로써 적절한 차분횟수까지 구할 수 있다 (Robert Nau @Duke university).

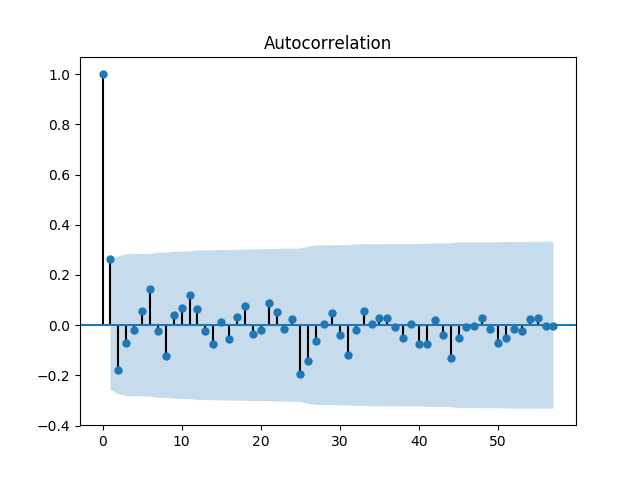
본 포스트에서는 python package인 statsmodels를 사용하여 ACF 및 PACF를 계산했으며, 비트코인 가격 자료의 ACF 및 PACF는 다음과 같다.

import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

plot_acf(series)
plot_pacf(series)
plt.show()

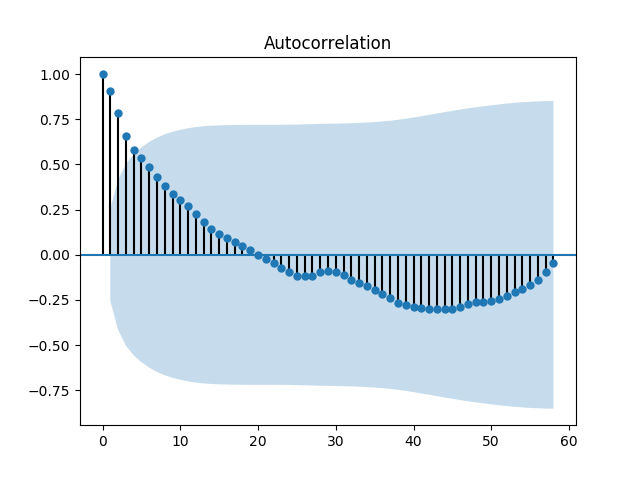
rawdata_acf
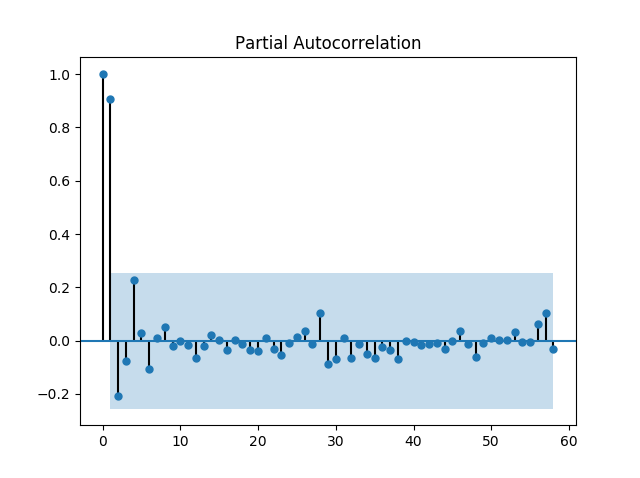
rawdata_pacf

ACF를 보면 20의 Time lag을 기준으로 자기상관이 양에서 음으로 변동한다. 또한 PACF는 1의 Time lag에서 약 0.9를 보이고 이후에 급격히 감소한다. 따라서 p=0, q=1이 적당하다고 추측할 수 있다.

적절한 차분 차수의 계산을 위해 우선 1차 차분을 하고, ACF 및 PACF를 다시 계산한다.

import matplotlib.pyplot as plt
import pandas as pd
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

diff_1=series.diff(periods=1).iloc[1:]
diff_1.plot()
plot_acf(diff_1)
plot_pacf(diff_1)
plt.show()

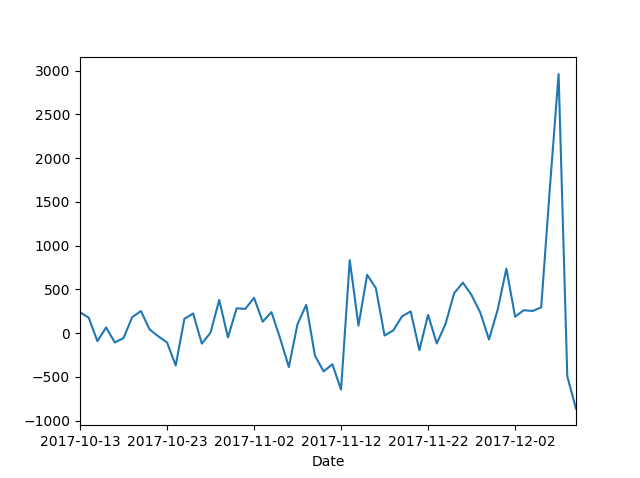
diff1_plot
diff1_acf
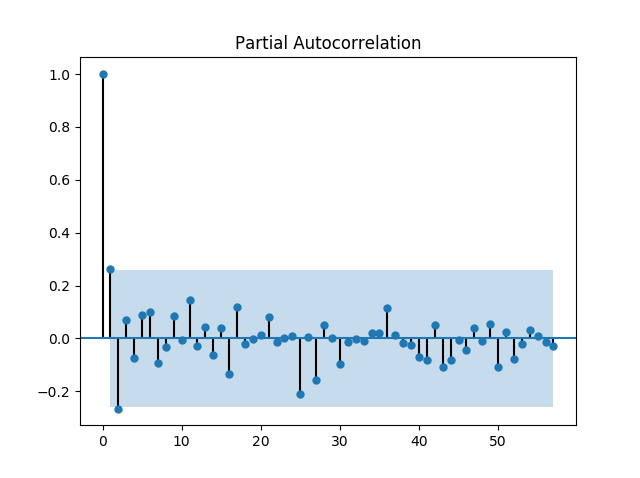
diff1_pacf

차분 결과를 보니, 12월 초에 있었던 급등락이 더 도드라져보인다…2500만원에 물리신분들께 애도..

아무튼, 차분이후의 ACF와 PACF를 보니, 시계열이 정상상태(Stationary)를 보이는것으로 생각되므로, 1차차분 만으로 충분할것같다.
따라서 본 데이터에는 ARIMA(0,1,1)을 사용하기로 한다.

모형구축

ARIMA(0,1,1)을 이용하여 모형의 Parameter를 추정하고, 결과를 확인한다.

from statsmodels.tsa.arima_model import ARIMA

model = ARIMA(series, order=(0,1,1))
model_fit = model.fit(trend='c',full_output=True, disp=1)
print(model_fit.summary())

                             ARIMA Model Results                              
==============================================================================
Dep. Variable:                D.Price   No. Observations:                   58
Model:                 ARIMA(0, 1, 1)   Log Likelihood                -442.285
Method:                       css-mle   S.D. of innovations            495.214
Date:                Wed, 13 Dec 2017   AIC                            890.570
Time:                        13:10:49   BIC                            896.751
Sample:                    10-13-2017   HQIC                           892.977
                         - 12-09-2017                                         
===================================================================================
                      coef    std err          z      P>|z|      [0.025      0.975]
-----------------------------------------------------------------------------------
const             166.9630     91.874      1.817      0.075     -13.107     347.033
ma.L1.D.Price       0.4200      0.131      3.199      0.002       0.163       0.677
                                    Roots                                    
=============================================================================
                 Real           Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
MA.1           -2.3811           +0.0000j            2.3811            0.5000
-----------------------------------------------------------------------------

‘P > z’ 값이 일반적으로 학습의 적정성을 위해 확인되는 t-test값이다. 즉, p value 0.05수준에서 보면 MA(1)의 계수는 유효하고, 모형의 Constant는 유효하지 않다…(슬픔)

따라서, 위 코드에서 model.fit()의 파라미터중 trend=’c’가 아니라 ‘nc’로 설정해주어야 하는게 옳다.

from statsmodels.tsa.arima_model import ARIMA

model = ARIMA(series, order=(0,1,1))
model_fit = model.fit(trend='nc',full_output=True, disp=1)
print(model_fit.summary())

                             ARIMA Model Results                              
==============================================================================
Dep. Variable:                D.Price   No. Observations:                   58
Model:                 ARIMA(0, 1, 1)   Log Likelihood                -443.856
Method:                       css-mle   S.D. of innovations            508.665
Date:                Wed, 13 Dec 2017   AIC                            891.712
Time:                        14:08:16   BIC                            895.833
Sample:                    10-13-2017   HQIC                           893.318
                         - 12-09-2017                                         
===================================================================================
                      coef    std err          z      P>|z|      [0.025      0.975]
-----------------------------------------------------------------------------------
ma.L1.D.Price       0.4514      0.123      3.657      0.001       0.209       0.693
                                    Roots                                    
=============================================================================
                 Real           Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
MA.1           -2.2152           +0.0000j            2.2152            0.5000
-----------------------------------------------------------------------------

예측

constraint가 없는 모형으로 fitting하고 나니, MA(1)의 t-test값이 0.001로 더 좋아졌다.
이제, 모형을 통해 예측된 값을 보자.

model_fit.plot_predict()

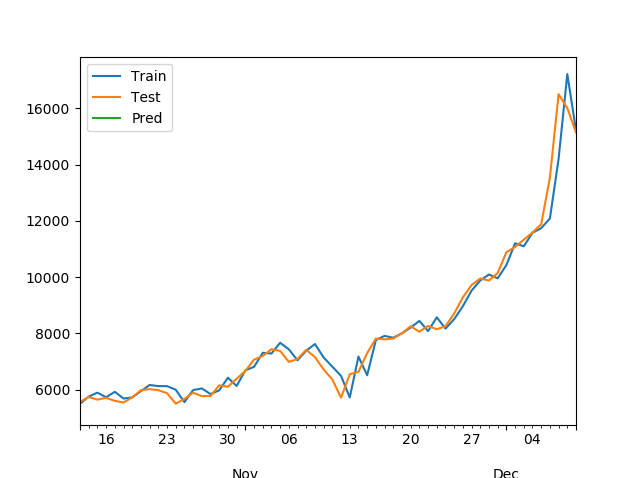
fitedvalue
fitting이 잘 된것으로 보인다.
또한, 앞으로의 값을 예측하기 위해서는 forecast method를 사용할 수 있다. 코드에서 steps는 예측할 개수를 의미한다.

fore = model_fit.forecast(steps=1)
print(fore)

위 코드의 결과는 아래와 같은데, 순서대로 예측값, stderr, upper bound, lower bound 이다.
(array([ 15061.16108756]), array([ 508.66521867]), array([[ 14064.19557878], [ 13303.94590548]]))
즉, 가장 즁요한 예측값은 15061달러인데, 학습에 쓰인 데이터가 12월 9일까지이므로, ARIMA모형은 12월 10일의 비트코인 가격을 15,061달러로 예측하였다.

참고로, 같은 사이트에서 획득한 12월 10일의 실제 비트코인 가격은 아래와 같다.
realvalue

마치며

최근 딥러닝, 인공지능 등의 트랜드와 함께 시계열분석에도 인공신경망이 널리 사용되고 있다.
특히 시계열분석에는 RNN, LSTM 등을 이용할 수 있지만, 신경망모델의 가장 큰 단점은 (아직까지는)제대로 된 모형해석이 거의 안된다는 점이다.
알고리즘적인 측면에서야 성능이 잘나오면 되는거지만 데이터과학, 특히 의사결정 지원 시스템(Decision support system)에서는 최종 결정권자는 사람이기에 모형이 그렇게 예측한 근거가 필요하다.
이러한 관점에서 보았을 때, AR, MA 등과 같은 고전적인 통계기반의 시계열분석법이 아직은 조금 더 우위에 있지 않나 한다.
(물론 신경망모형이 대부분 컴퓨터비전이나 자연어처리에 신경쓰고 있기 때문에 시계열모형 그 자체로써 고려는 아직 부족한 점도 한몫 한다.)

ARIMA에 관해 통계적 기반이나 지식을 포함하여 더 알고싶다면 위에서 언급한 Box, George; Jenkins, Gwilym (1970). Time Series Analysis: Forecasting and Control. 이나, Robert Nau @Duke university의 강의자료를 참고하면 좋다.